Протокол диффи
Содержание:
- Время шифрования!
- Что такое методика Диффи-Хеллмана?
- Практические рекомендации
- Алгоритм Диффи-Хеллмана: обзор
- Протокол Диффи — Хеллмана для конференц-связи
- Описание алгоритма[2]
- Пример
- Алгоритм Диффи-Хеллмана: назначение
- Генерация полного ключа
- Прошлое: классический Диффи-Хеллман
- Источники
- Подводные камни
- Первый алгоритм DH
- Предпосылки создания алгоритма Диффи-Хеллмана
- Краткая математика: группы
- Частичный обмен ключами
Время шифрования!
Теперь, когда у нас есть общий ключ шифрования, пришло время начать обмен сообщениями! Как объяснялось в начале этого раздела, Майкл хочет отправить мне зашифрованное сообщение. Вот простой алгоритм, который я написал для шифрования сообщения Майкла:
Ничего особенного. Каждый символ кодируется в целое число, значение ключа добавляется, а затем целое число преобразуется обратно в символ. Этот процесс повторяется для каждого символа в сообщении. Первоначальное сообщение, которым хотел поделиться Майкл: «This is a very secret message!!!». Давайте добавим его в алгоритм с нашим новым ключом шифрования.
Прим. пер.: это шифр простой замены, которым в реальной жизни пользоваться не стоит. Взламывается чуть сложнее классического, но всё равно достаточно быстро.
Зашифрованное сообщение — «», что при чтении выглядит как бессвязный набор символов. Мистер Робот понятия не имеет, чем Майкл делится со мной по сети.
Теперь пришло время расшифровать сообщение с моей стороны.
Эта функция делает обратное преобразование. На этапе шифрования было добавлено значение ключа, на этапе расшифровки будет вычтено то же самое значение.
Получил сообщение! Хорошая попытка, Мистер Робот. Нам удалось обмениваться зашифрованными сообщениями, не поставив под угрозу наши ключи шифрования.
Удачи с Evil Corp!
Программист
«ООО «ОЛКОН»», Самара, от 30 000 ₽
tproger.ru
Вакансии на tproger.ru
Мы рассмотрели механику работы алгоритма Диффи-Хеллмана на примерах с цифрами и кодом на Python. Если вы хотите закрепить полученные знания, будет полезно посмотреть это видео:
Что такое методика Диффи-Хеллмана?
Если подходить к вопросу о самом алгоритме, пока, не вдаваясь в технические и математические подробности, можно определить его как методику шифрования и дешифровки передаваемой и принимаемой информации между двумя и более пользователями компьютерных или других систем, предполагающих обмен данными с использованием незащищенного канала связи.
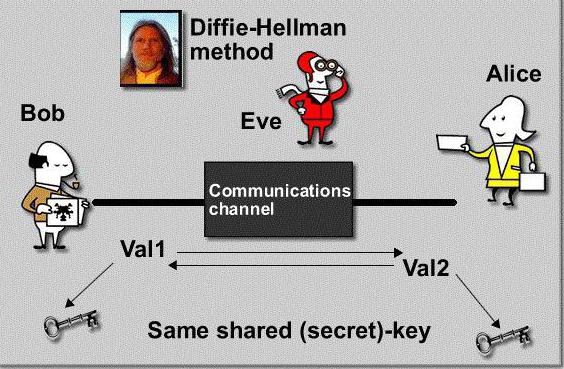
Как уже понятно, при отсутствии защиты самого канала перехватить или модифицировать файлы, находящиеся в процессе передачи-приема, может и злоумышленник. Однако алгоритм распределения ключей Диффи-Хеллмана для доступа к передаваемым и принимаемым данным таков, что постороннее вмешательство практически полностью исключается. При этом общение по используемому каналу связи (без защиты оного) становится безопасным, если обе стороны используют один и тот же ключ.
Практические рекомендации
Приведем несколько практических советов относительно использования протокола DH. Выбирать в качестве k следует простое число размером 256 бит. Это минимум, который способен обеспечить хоть сколько-то адекватный уровень безопасности против атак. В качестве a выбрать число, которое имело бы вид Na+1, где N — некоторое целое число. О размерах числа a было сказано ранее. После этого выбирается случайное число b и проверяется на несколько условий. Во-первых, оно не может быть единицей. Во-вторых, bk = 1.
В свою очередь, любой участник общения должен убедиться в следующем:
- a и k — простые числа, длина k составляет 256 бит, длина p достаточно велика.
- число k является делителем a-1.
- b не равно 1 и bk = 1.
Данные условия следует проверять даже при безоговорочном доверии к источнику.
Алгоритм Диффи-Хеллмана: обзор
Итак, сам алгоритм подразумевает использование нескольких базисных понятий. Допустим, у нас имеется простейший случай, когда на связи присутствуют два абонента (пользователя). Обозначим их как A и B.
Они используют два числа X и Y, не являющиеся секретными в данном канале связи, для управления приема-передачи. Вся суть вопроса сводится к тому, чтобы сгенерировать на их основе некое новое значение, которое будет являться ключом. Но! Первый абонент использует большое простое число, а второй – обязательно целое (делящееся без остатка), но меньшее по порядку, чем первое.
Естественно, пользователи договариваются, что эти числа хранятся в тайне. Однако, поскольку канал связи является незащищенным, эти два числа могут стать известными и другим заинтересованным лицам. Именно поэтому пользователи в тех же сообщениях обмениваются секретными ключами для расшифровки сообщений.
Протокол Диффи — Хеллмана для конференц-связи
Разновидность протокола используемого при общении трех и более участников.
Участники:
A,B,C{\displaystyle ~A,B,C}
- Agx(modp)→B{\displaystyle ~A:g^{x}{\pmod {p}}\rightarrow B},где p{\displaystyle ~p} — простое, g{\displaystyle ~g} — первообразный корень.
- By=gy(p)→C{\displaystyle ~B:y=g^{y}(p)\rightarrow C}
- Cz=gz(p)→A{\displaystyle ~C:z=g^{z}(p)\rightarrow A}
- Az′=zx(p)→B{\displaystyle ~A:z’=z^{x}(p)\rightarrow B}
- Bx′=xy(p)→C{\displaystyle ~B:x’=x^{y}(p)\rightarrow C}
- Cy′=yz(p)→A{\displaystyle ~C:y’=y^{z}(p)\rightarrow A}
{k=y′x(p)k=z′y(p)k=y′z(p) ⇒ k=gxyz(modp){\displaystyle ~{\begin{cases}k=y’^{x}(p)\\k=z’^{y}(p)\\k=y’^{z}(p)\end{cases}}\ \Rightarrow \ k=g^{xyz}{\pmod {p}}}
Описание алгоритма[2]
Предположим, существует два абонента: Алиса и Боб. Обоим абонентам известны некоторые два числа g{\displaystyle g} и p{\displaystyle p}, которые не являются секретными и могут быть известны также другим заинтересованным лицам. Для того, чтобы создать неизвестный более никому секретный ключ, оба абонента генерируют большие случайные числа: Алиса — число a{\displaystyle a}, Боб — число b{\displaystyle b}. Затем Алиса вычисляет остаток от деления (1):
A=gamodp{\displaystyle A=g^{a}{\bmod {p}}} (1)
и пересылает его Бобу, а Боб вычисляет остаток от деления (2):
B=gbmodp{\displaystyle B=g^{b}{\bmod {p}}} (2)
и передаёт Алисе. Предполагается, что злоумышленник может получить оба этих значения, но не модифицировать их (то есть, у него нет возможности вмешаться в процесс передачи).
На втором этапе Алиса на основе имеющегося у неё a{\displaystyle a} и полученного по сети B{\displaystyle B} вычисляет значение (3):
Bamodp=gabmodp{\displaystyle B^{a}{\bmod {p}}=g^{ab}{\bmod {p}}} (3)
Боб на основе имеющегося у него b{\displaystyle b} и полученного по сети A{\displaystyle A} вычисляет значение (4):
Abmodp=gabmodp{\displaystyle A^{b}{\bmod {p}}=g^{ab}{\bmod {p}}} (4)
Как нетрудно видеть, у Алисы и Боба получилось одно и то же число (5):
K=gabmodp{\displaystyle K=g^{ab}{\bmod {p}}} (5)
Его они и могут использовать в качестве секретного ключа, поскольку здесь злоумышленник встретится с практически неразрешимой (за разумное время) проблемой вычисления (3) или (4) по перехваченным gamodp{\displaystyle g^{a}{\bmod {p}}} и gbmodp{\displaystyle g^{b}{\bmod {p}}}, если числа p{\displaystyle p}, a{\displaystyle a}, b{\displaystyle b} выбраны достаточно большими. Наглядная работа алгоритма показана на рисунке.
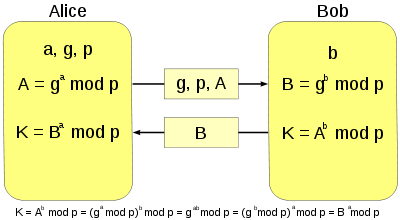
Алгоритм Диффи — Хеллмана, где K — итоговый общий секретный ключ
При работе алгоритма каждая сторона:
- генерирует случайное натуральное число a — закрытый ключ
- совместно с удалённой стороной устанавливает открытые параметры p и g (обычно значения p и g генерируются на одной стороне и передаются другой), где
- p является случайным простым числом
- (p-1)/2 также должно быть случайным простым числом (для повышения безопасности)
- g является первообразным корнем по модулю p (также является простым числом)
- вычисляет открытый ключ A, используя преобразование над закрытым ключом
- A = gamod p
- обменивается открытыми ключами с удалённой стороной
- вычисляет общий секретный ключ K, используя открытый ключ удаленной стороны B и свой закрытый ключ a
- K = Bamod p
- К получается равным с обеих сторон, потому что:
- Bamod p = (gbmod p)amod p = gabmod p = (gamod p)bmod p = Abmod p
В практических реализациях для a и b используются числа порядка 10100 и p порядка 10300. Число g не обязано быть большим и обычно имеет значение в пределах первого десятка.
Пример
Ева — криптоаналитик. Она читает пересылку Боба и Алисы, но не изменяет содержимого их сообщений.
- s = секретный ключ. s = 2
- g = первообразный корень по модулю р. g = 5
- p = открытое простое число. p = 23
- a = секретный ключ Алисы. a = 6
- A = открытый ключ Алисы. A = ga mod p = 8
- b = секретный ключ Боба. b = 15
- B = открытый ключ Боба. B = gb mod p = 19
|
|
|
Алгоритм Диффи-Хеллмана: назначение
Сам алгоритм создавался таким образом, чтобы обеспечить не только конфиденциальность данных при передаче одной стороной другой, но и для того, чтобы безопасно извлечь их при получении. Грубо говоря, такая система передачи должна обеспечить полноценную защиту по всем возможным каналам общения.

Вспомните хотя бы годы Второй мировой войны, когда разведки всех стран-союзников безуспешно охотились за шифровальной машиной под названием «Энигма», с помощью которой передавались кодированные сообщения на азбуке Морзе. Ведь ее шифр не мог разгадать ни один, даже самый, как мы сейчас говорим, «продвинутый» специалист по криптографии. Только после ее захвата был получен ключ к дешифровке сообщений, передаваемых немецким флотом.
Генерация полного ключа
Теперь, когда мы успешно обменялись частичными ключами, давайте снова применим операторы степени и деления с остатком к частичному ключу другого человека, используя наши собственные закрытые ключи следующим образом:
Реализация этого в Python:
Код с моей стороны:
И то же самое для Майкла, использующего мой частичный ключ:
Сравнивая их:
Заметили что-нибудь интересное? Мы оба получили одинаковые полные ключи, равные ! Причина заключается в следующем математическом соотношении:
Здесь и — закрытые ключи, а и — открытые. Нам удалось обменяться друг с другом по сети достаточным количеством информации, чтобы сгенерировать общий ключ шифрования, не ставя под угрозу наши закрытые ключи.
Прошлое: классический Диффи-Хеллман
Алиса и Боб изначально выбирают параметры (domain parameters): мультипликативную группу конечного поля и g — генератор ее подгруппы. Ничего страшного в слове генератор нет. Это всего лишь один из элементов группы со следующим свойством: если взять его степени от 1 до числа элементов группы, мы получим всю группу целиком. Подгруппа – это подмножество группы, которая сама по себе – тоже группа (при перемножении ее элементов в любых сочетаниях, мы получим только элементы этого самого подмножества).
Пример:
Элементы группы:
числа от 1 до p — 1, где p – простое число.
Групповая операция a*b mod p: умножаем элементы группы a и b, затем a*b делим на p. Остаток от деления a*b на p и есть результат операции a*b mod p.
К примеру, пусть модуль p равен 11. Чаще всего обозначается как . Состоит из 11 – 1 = 10 элементов: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10
Число элементов в группе называется порядком группы (group order). Порядок равен 10.
А теперь немного поиграем с операциями:
1 для этой группы – это нейтральный элемент. Neutral — т.к. он “не взаимодействует” ни с какими другими элементами и результат операции с ним всегда равен второму элементу операции. В данном случае 1*10 mod 11 — это 10.
Для любого элемента любой группы существует обратный элемент, который “обращает” его в нейтральный. Для этой группы 6 и 2 – обратные друг для друга.
Когда групповая операция называется умножением (как в случае ), то используют такие обозначения для обратного к элемента: Т.е. * = 1 Что еще можно сказать про эту группу? Она коммутативна (или абелева):
Генераторы группы — это такие ее элементы, все степени которых являются всеми элементами группы. Группы, в которых есть хотя бы один такой элемент называют циклическими. Как понять, что x – генератор? Самый примитивный метод: построить таблицу степеней x:
Как насчет степеней 2?
Итого: 2 — генератор .
Порядок элемента – минимальная степень, в которую его надо возвести, чтобы получить нейтральный. Порядок 2 в равен 10.
Теперь рассмотрим степени 3:
Порядок 3 равен 5. Он не “пробегает” все значения , т.к. мы видим, что на пятой степени происходит зацикливание: если продолжить умножение, то опять получим 3, 9, 5, 4, 1.
Что еще можно сказать про 3?
Легко видеть, что это подмножество -подгруппа: есть нейтральный элемент 1. Замкнутость: результат любых a*b mod p для этих чисел не выходит за пределы этого множества, ведь результат будет одним из множества {3, 9, 5, 4, 1}.
Каждый элемент имеет обратный: 3*4 mod 11 = 1, 9*5 mod 11 = 1, 1*1 mod 11 = 1. Какие еще подгруппы есть в ?
Еще есть группа порядка 2: {1, 10}
Ну и конечно же тривиальные подгруппы { 1 } и {1, 2, 3, 4, 5, 6, 7, 8, 9, 10} (т.к. формально группа является подгруппой самой себя)
Как можно оптимизировать поиск генератора для ?
Тут необходимо использовать фундамент теории групп – теорему Лагранжа: “Порядок подгруппы делит порядок группы”.
Элемент x либо является генератором группы, либо является генератором одной из ее подгрупп. Следовательно, возведение x в степени порядков подгрупп и сравнение результата с 1 может это подтвердить или опровергнуть.
Примечание: Алисе и Бобу необходимо проверять приходящие извне ключи на принадлежность их “рабочей” подгруппе большого простого порядка q:
Алиса проверяет mod p = 1? Если нет, то протокол прерывается.
Аналогично поступает Боб: он проверяет ключ, пришедший от Алисы: mod p = 1?
Мы сейчас не рассматриваем противника, который мог бы подменить по дороге открытые ключи, но тем не менее всегда надо помнить, что и в криптографии встречаются случаи из разряда “при таких друзьях нам и враги не нужны”: программа на устройствах Алисы или Боба может содержать различные ошибки (в реализации модульной арифметики, или просто может повредиться память).
Источники
- Брюс Шнайер. Прикладная криптография
- Мао, В. Современная криптография: теория и практика. : Пер. с английского. М.: Издательский дом «Вильямс», 2005. — 768 с. : ил. — Парал. тит. англ. Шифрование — асимметричные методы. Глава 8 («Шифрование с открытым ключом», «Обмен ключом без обмена ключом», «Криптографическая стойкость», «Задача Диффи — Хеллмана и задача дискретного логарифмирования»)
- Dieter Gollmann (2006). Computer Security Second Edition West Sussex, England: John Wiley & Sons, Ltd.
- T. Kivinen; M. Kojo, SSH Communications Security. (англ.) (TXT). Standards Track. Инженерный совет Интернета (May 2003). — Стандартные группы открытых чисел p и g, рекомендуемые Инженерным советом Интернета (IETF). Дата обращения 15 февраля 2016.
- The possibility of Non-Secret digital encryption J. H. Ellis, January 1970.
- Non-Secret Encryption Using a Finite Field MJ Williamson, January 21, 1974.
- Thoughts on Cheaper Non-Secret Encryption MJ Williamson, August 10, 1976.
- New Directions in Cryptography W. Diffie and M. E. Hellman, IEEE Transactions on Information Theory, vol. IT-22, Nov. 1976, pp: 644—654.
- Cryptographic apparatus and method Martin E. Hellman, Bailey W. Diffie, and Ralph C. Merkle, U.S. Patent #4,200,770, 29 April 1980
- The History of Non-Secret Encryption JH Ellis 1987 (28K PDF file) (HTML version)
- The First Ten Years of Public-Key Cryptography Whitfield Diffie, Proceedings of the IEEE, vol. 76, no. 5, May 1988, pp: 560—577 (1.9MB PDF file)
- Menezes, Alfred; van Oorschot, Paul; Vanstone, Scott (1997). Handbook of Applied Cryptography Boca Raton, Florida: CRC Press. ISBN 0-8493-8523-7. (Available online)
- Singh, Simon (1999) The Code Book: the evolution of secrecy from Mary Queen of Scots to quantum cryptography New York: Doubleday ISBN 0-385-49531-5
- An Overview of Public Key Cryptography Martin E. Hellman, IEEE Communications Magazine, May 2002, pp: 42—49. (123kB PDF file)
- Diffie-Hellman key exchange explained in 5 minutes
- Oral history interview with Martin Hellman, Charles Babbage Institute, University of Minnesota. Leading cryptography scholar *Martin Hellman discusses the circumstances and fundamental insights of his invention of public key cryptography with collaborators Whitfield Diffie and Ralph Merkle at Stanford University in the mid-1970s.
- Summary of ANSI X9.42: Agreement of Symmetric Keys Using Discrete Logarithm Cryptography (64K PDF file) (Description of ANSI 9 Standards)
- Diffie-Hellman Key Exchange — A Non-Mathematician’s Explanation by Keith Palmgren
- Crypt::DH Perl module from CPAN
- Hands-on Diffie-Hellman demonstration
- C implementation using GNU Multiple Precision Arithmetic Library
- Diffie Hellman in 2 lines of Perl (using dc)
- Smart Account Management (SAcct) (using DH key exchange to derive session key)
- Talk by Martin Hellman in 2007, Google video
Подводные камни
Помимо атаки посредника протокол DH таит в себе массу других проблем. Например, одним из недостатков является случай, когда в роли образующего числа a выступает не примитив. Тогда он порождает лишь подгруппу. Из-за сужения количество возможных вариантов злоумышленнику открывается возможность их перебора.

Проблем из-за этого недочета можно избежать, если каждый из собеседников перед началом обмена данными будет проверять, что числа a и b выбраны правильно. То есть a является простым числом, а b — примитивом. Однако когда дело доходит до соблюдения безопасности посредством выполнения определенных однообразных необязательных шагов, пользователи часто их игнорируют.
Другая серьезная проблема возникает на основе подгрупп по модулю a. Если злоумышленник решит поменять gx на 1, чтобы облегчить себе процесс подслушивания, то пользователи смогут легко его обнаружить, проверив число на соответствие. Однако, если он подменит ключ числом с низким порядком, пользователи не смогут ничего заподозрить. А так как количество элементов в множестве с низким порядком будет невелико, то злоумышленнику для расшифровки нужно будет перебирать небольшое количество вариантов.
Первый алгоритм DH
В первоначальной версии алгоритм работал по следующей схеме. Выбираются большое число a из множества простых и примитивный элемент b, порождающий Z*a. Оба числа a и b представляют собой открытый ключ, они известным всем, в том числе и злоумышленникам. Как же тогда скрыть сообщения?
Именно на этом шаге Диффи и Хеллман придумали очень остроумный ход. Пусть у нас есть два человека, связывающихся между собой: А и Б. Сначала А выбирает случайное число x из Z*a , что является эквивалентом выбора числа из {1, …, a-1}. Затем он вычисляет значение по формуле (bx mod a) и отправляет его Б. В свою очередь Б выбирает некоторое число y из того же множества, вычисляет значение (by mod a) и отправляет результат обратно А.

Таким хитрым способом получается, что секретный ключ выглядит bxy . Благодаря свойству степеней, которое гласит gxy = (gy)x, собеседник А может вычислить нужное значение и расшифровать пересланную ему информацию. И точно так же это значение вычисляет собеседник Б. Таким образом, оба имеют одинаковый секретный ключ.
Какие проблемы испытывает злоумышленник при таком обмене информацией? Он может перехватить числа gx и gy. И даже при знании открытых ключей задача вычисления gxy не является тривиальной, т. к. пока не существует эффективного алгоритма поиска нужного значения в распределении ключей Диффи-Хеллмана. Данная задача известна под названием «проблема вычисления дискретного логарифма».
Предпосылки создания алгоритма Диффи-Хеллмана
Аутентификация и шифрование до этого момента были возможны лишь посредством общего секретного ключа. С развитием технологий вопрос становился более острым. Если 10 людям необходим передавать данные между собой по небезопасным каналам, им потребуется обмениваться паролями друг с другом. Данная задача выглядит вполне реальной. Даже с учетом необходимости их обновления. Ведь для 10 друзей понадобится всего 45 секретных ключей. А если контактов будет 100? Понадобится 4950 паролей. Ситуация нарастает как снежный ком.
Главным достижением Диффи и Хеллмана стала правильная постановка вопроса и остроумный ответ на него. Они предположили, что данные можно шифровать одним способом, а расшифровывать — другим. То есть иметь 2 ключа. Тот, что используется для шифрования, можно оставить открытым. Таким образом любой человек сможет зашифровать сообщение, но расшифровать смогут его только обладатели второго секретного ключа. Но как реализовать алгоритм передачи такого ключа? Ученые смогли частично и на это дать ответ.
Краткая математика: группы
Алгоритм или протокол Диффи-Хеллмана (далее DH) работает при помощи простых чисел. Пусть а — это достаточно большое число, принадлежащее множеству простых чисел. Алгоритм предполагает использование числа размером 250-500 байт. Пусть Zа — мультипликативная группа кольца вычетов по модулю а, которая будет использована алгоритмом шифрования Диффи-Хеллмана. Она состоит из множества чисел 1, …, a-1.
Возьмем некий элемент b из группы Zа и рассмотрим бесконечную последовательность 1, b, b2, b3, b4, … Из того факта, что группа Za по определению является конечным множеством, рано или поздно рассматриваемая последовательность {b} начнет повторяться. Положим bi = bj (i < j).
Теперь разделим каждую часть равенства на bi (по модулю a) и получим bj-i = 1. Это значит, что существует такое число k = j-i, для которого верно bk = 1 (mod a). Самое маленькое число k, для которого выполняется данное равенство, называется порядком числа b. Во избежание недопонимания с другой специальной литературой для объяснения системы Диффи-Хеллмана используются стандартные математические обозначения.

Таким образом, возводя число b, называемое образующим элементом, в степень, мы получаем последовательность чисел (множество) 1, …, bk-1 . Количество элементов данного множества в точности равно k.
Свойство умножения по модулю a гласит, что существует хотя бы одно число b, порождающее все элементы группы Z*a . Иначе говоря существует число для которого верно k = a — 1. Данное свойство позволяет представить числа группы Z*a в виде 1, b, b2, … ba-2 . Такое число b называется примитивным числом группы.
В дальнейшем по признакам группы легко доказывается, что множество, порожденное числом b, также само является группой и наследует все свойства групп. Иными словами, операции внутри порожденной группы или подгруппе можно проводить точно таким же образом, как в группе по модулю a.
Рассмотрим утверждение. Для любого элемента b его порядок является делителем числа a-1. Это легко показать. Пусть a=7. Число b = 3 — примитивное, т. к. 1, …, b5 = 1, 3, 2, 6, 4, 5. Тогда число h = 2 будет порождать подгруппу 1, …, h2 = 1, 2, 4, так как h3 = 23 mod 7 = 1. h = 6 порождает подгруппу 1, 6. Размеры групп равны 3 и 2, соответственно. Очевидно, что они являются делителями числа a-1 = 6.
Частичный обмен ключами
Давайте предположим, что мы ничего не видим внутри сервера Майкла (включая его личный ключ).
Теперь мне нужно создать частичный ключ шифрования, используя 3 доступные единицы информации: мой закрытый и открытый ключи и открытый ключ Майкла. Алгоритмически мы согласились использовать мой открытый ключ в качестве базы и его открытый ключ в качестве модуля.
Если мы посмотрим на нашу функцию для генерации частичного ключа, то она именно эти вычисления и делает:
Теперь давайте сгенерируем этот частичный ключ и отправим его Майклу по сети.
Таким же образом Майкл посылает мне свой частичный ключ по сети.
Сравнение обоих вычислений частичного ключа:
Мистер Робот, естественно, увидел обмен частичными ключами. Он также знает оба открытых ключа. Теперь ему нужно взломать наши соответствующие закрытые ключи.
Всё, что знает Мистер Робот, — это частичные ключи и соответствующие открытые ключи, а также формула, используемая для получения частичных ключей. Особенность вычисления по модулю в том, что функция заставляет значение циклически изменяться. Если у вас есть модуль , значение будет между и .
Существует бесконечное число возможных значений, которые по модулю будут равны либо , либо . В результате информации для получения закрытых ключей пользователей недостаточно (если не считать грубый перебор безумно большого числа всевозможных вариантов). Кроме того, в примере используются небольшие числа для закрытых и открытых ключей, что делает подбор реальным. В реальной жизни это было бы почти невозможно!